Caracterizando Estruturas de Dados


Ainda vejo os desenvolvedores, independente da senioridade, com muitas dificuldades de identificar as caraterísticas da melhor estrutura de dados (provida pela linguagem) que pode, ou deve, ser usada para resolver determinado algoritmo ou problema.
Boa parte desta dificuldade vem de não conseguir diferenciar intrinsecamente as características de cada uma delas.
Este post vai procurar explorar as estruturas básicas, bem como finalizar com um exemplo de como uma estrutura de dados correta pode otimizar MUITO um algoritmo.
Critérios de caracterização
Antes de falar das estruturas de dados e coleções em si, vamos falar sobre critérios para classificá-las. Essencialmente podemos usar três critérios:
- Noção de ordem
- Noção de repetição
- Acesso (de um elemento individual)
Noção de ordem
A “noção de ordem”, ou “ordenação”, refere-se ao fato de os elementos da coleção se caracterizarem como “em ordem”, ou seja, podemos raciocinar como “o primeiro elemento da coleção”, “o segundo”, “o terceiro”, “o último”, “o penúltimo” ou ainda “este elemento está antes daquele” ou “este está duas posições antes daquele”, e assim por diante.
Observe que a noção de ordem em software engineering não é a necessariamente a mesma noção de ordem da matemática. Noção de ordem presume noção de comparação sobre os índices, ou seja, podemos dizer que um índice é menor, igual ou maior que outro.
Quando pensamos em números (naturais), a “ordem natural” vem imediatamente na cabeça. 1, 2, 3, ..., estabelecem a ordem que todos aprendemos na escola. Com strings, acontece o mesmo com a “ordem alfabética”. Mas, em programação, temos muito a noção de “ordem parcial”. Em primeiro lugar porque existe o null/nil e o null não é comparável naturalmente (podemos estabelecer uma convenção que null vem antes ou depois dos elementos não nulos, mas isso é uma convenção arbitrária).
Em segundo lugar, porque quando estabelecemos um tipo composto (exemplo: uma classe VO – Value Object -- com dois campos, um String e um int, ou dois números, etc.), a noção de comparação não está pronta e normalmente temos que implementá-la.
Noção de repetição
A “noção de repetição” determina se os elementos podem ou não INTRINSECAMENTE estarem repetidos dentro de uma coleção.
Quando aprendemos conjuntos na escola, temos a definição intrínseca de uma coleção de “coisas” que não se repetem. O conjunto de números naturais não tem “dois números 2”. Temos o conjunto de alunos de uma sala de aula, o conjunto de vogais do alfabeto, ...
Mas, espera, você pode dizer, na chamada dos alunos existe a ordem em que eles são chamados, as vogais são (‘a’, ‘e’, ‘i’, ‘o’, ‘u’) nessa ordem! Nem tanto. Podemos estabelecer uma “ordem por fora”, a ordem alfabética do nome dos alunos ou das letras nesses dois exemplos, mas o conjunto intrinsecamente não tem ordem. Para outros fins como “sortear um aluno para resolver um exercício” ou “escolher uma vogal para iniciar uma palavra”, a ordem não é significativa.
De maneira geral quase todos os elementos de um conjunto podem ter uma “ordem artificial”. Em programação, mais uma vez, isso pode ser ainda mais necessário, por causa dos tipos compostos. Voltamos a isso logo mais.
Acesso (de um elemento individual)
Aqui estamos falando em como “chegamos” em um valor determinado de uma coleção, cuja determinação temos de antemão. Para coleções com ordem, a posição na coleção é esse critério. Quando falamos “pegue o quinto elemento da lista”, queremos ir “direto” no quinto elemento, ou no elemento de índice 4, para estruturas de dados “zero-based”, como os arrays em C ou Java. Para mapas, temos o acesso de um “valor” pela “chave”, e isso não depende de as chaves estarem em ordem. O modelo mental é a associação direta entre a chave e o valor correspondente. Veremos a seguir.
Tá enrolando muito; classifica logo!
As tabelas a seguir resumem como classificar as principais estruturas de dados baseadas nos critérios de ordem e repetição:
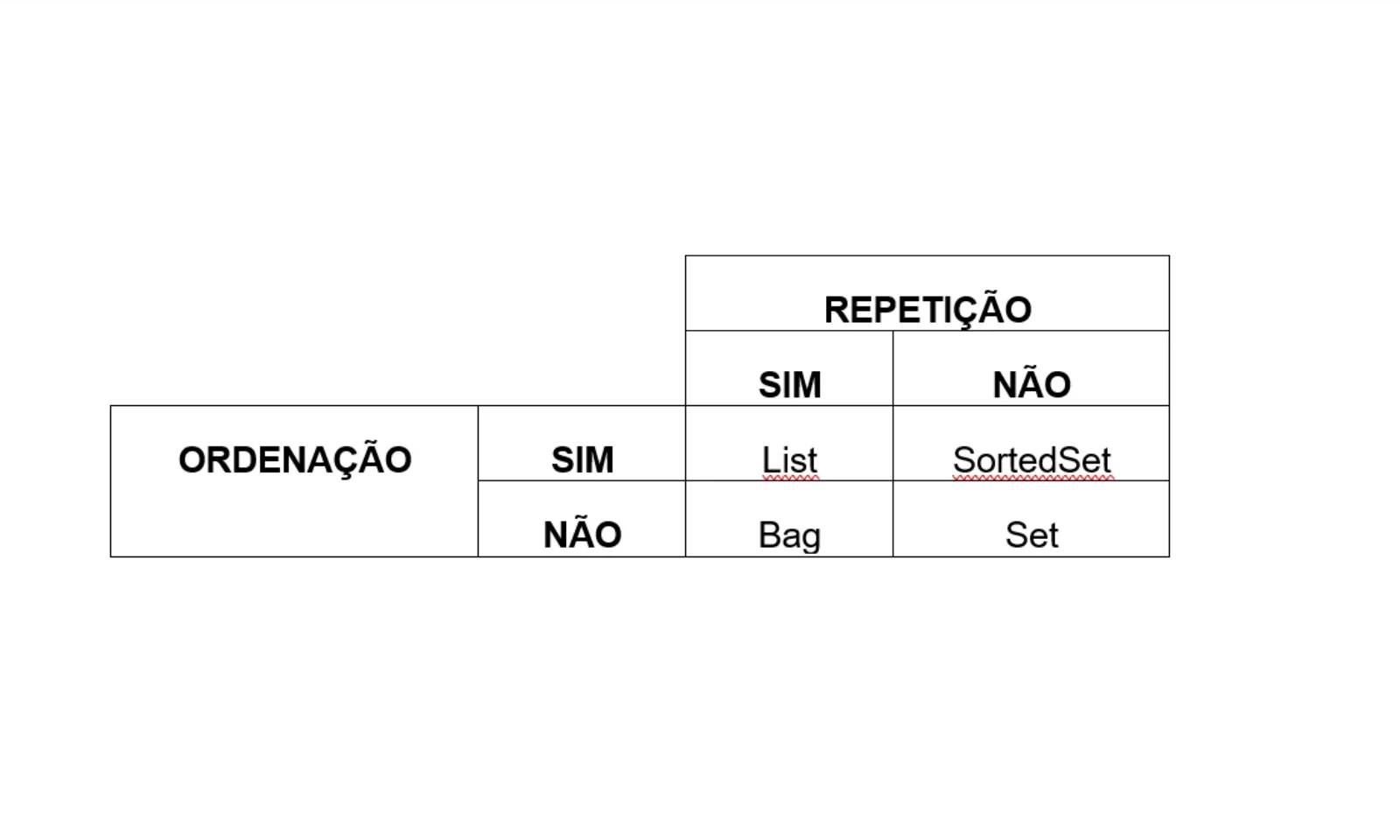
Lists
As listas são estruturas de dados ou coleções caracterizadas pela noção de ordem e pela possibilidade de repetição. Em havendo noção de ordem, existe o acesso pela posição, ou pelo índice. Ou seja, dado um índice, um número inteiro (0, 1, 2, ...) podemos acessar o valor na coleção pelo índice correspondente (sem entrar no mérito do índice além do comprimento da lista).
Quando dizemos que pode haver repetição, queremos dizer que o “o quarto elemento da lista pode ser igual ao sétimo”, ou seja, a coleção pode ter dois elementos iguais em posições diferentes.
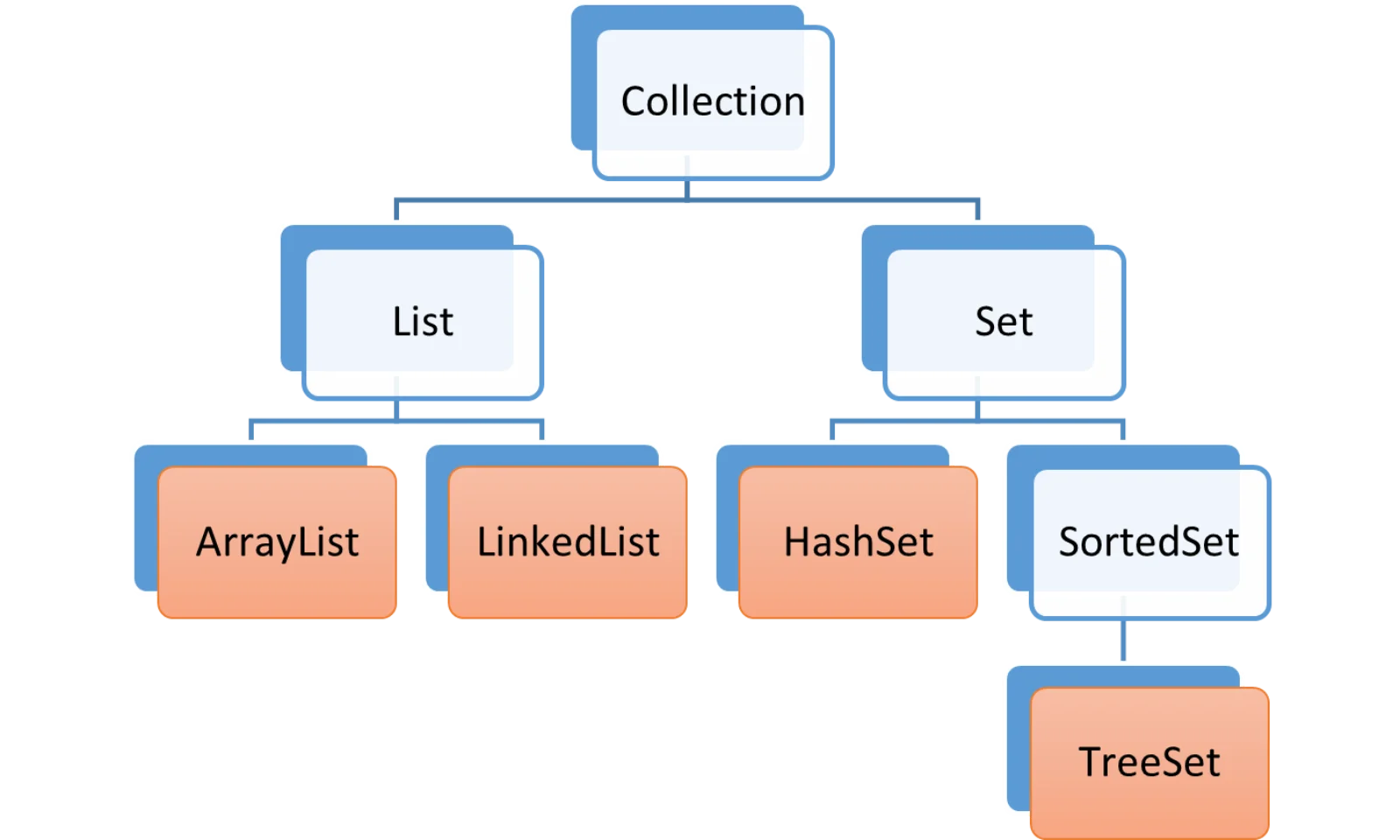
Atenção: o fato de podermos ter o acesso “direto” pelo índice, não quer dizer que esse acesso tem a mesma performance conforme a implementação da lista. Em Java, por exemplo, um ArrayList é uma lista implementada com um array (não diga!) como base e os acessos por índice são ultrarrápidos, em tempo constante. Um LinkedList é uma lista implementada com uma lista ligada como base, e os acessos por índice acontece com tempo linear no pior caso, proporcional ao comprimento da lista.
Sets
Os “sets”, ou conjuntos, são opostos das listas nessa classificação. São caracterizados por serem uma estrutura de dados, ou coleção, onde não existe a noção de ordem (ao menos, não intrinsecamente) e por não permitirem repetição.
Sets são o que mais se aproximam do que aprendemos em conjuntos nas aulas de matemática da escola e carregam justamente essas propriedades. Podemos perguntar o tamanho de um conjunto (o que caracteriza o número de elementos dele, já que não há repetições) e podemos perguntar se um elemento pertence ou não pertence ao conjunto.
Mas não podemos fazer uma operação como “pegar o terceiro elemento” do conjunto. Na verdade, formular essa frase para conjuntos já não faz sentido. Não existe o “terceiro” elemento de um conjunto não ordenado.
Também podemos pensar na união, intersecção e diferença, ou outras operações entre conjuntos.
Para os programadores Java, em particular, procurem a biblioteca “Apache Commons Collections” e a classe “SetUtils”, que têm muitas operações como essas já implementadas.
SortedSets
Quando queremos que uma coleção não permita elementos repetidos mas preserve a noção de ordem, os “SortedSet”s são a resposta.
Tudo que podemos fazer com Sets, podemos fazer com SortedSets. Em Java, de fato, a interface SortedSet<T> herda de Set<T>. Isso não quer dizer que você sempre deva escolher SortedSets, porque manter a ordenação tem custo.
Em Java, procure o javadoc da interface java.util.SortedSet para verificar as operações a mais disponíveis para conjuntos ordenados. Em particular, ao iterar os elementos de um conjunto ordenado, teremos a garantia de que eles serão iterados na ordem desejada.
E esse “Bag” aí que não tem na linguagem?
Bags são estruturas de dados que não possuem noção de ordem, mas possuem a noção de repetição. Talvez nas aulas de probabilidade ou estatística básica, você tenha visto problemas parecidos com o seguinte:
“Uma urna opaca possui sete bolas idênticas em tamanho e peso, quatro amarelas e três verdes. Ao retirar duas bolas, qual a probabilidade de saírem duas bolas verdes?”
Calma, você não precisa responder à questão acima. O que importa aqui é que essa “urna opaca” é um Bag.
Do ponto de vista da não-repetição, o Bag é praticamente um conjunto. Dá pra mais ou menos dizer que ele é mais parecido com um conjunto do que com uma lista. Mas a noção de poder repetir significa que, para cada elemento do “conjunto” (ênfase nas aspas aqui), o Bag carrega a quantidade de elementos (repetições) daquele tipo.
No exemplo da urna acima, podemos dar duas interpretações. Podemos dizer que o Bag tem 7 elementos. Ou podemos dizer que ele tem dois “tipos de elemento”, onde o primeiro tipo tem quantidade 4 e o segundo tem quantidade 3. Seu problema do mundo real é que dirá qual interpretação é mais aderente.
Mais um ponto de atenção para os javeiros: não existe uma interface Bag na hierarquia de coleções da linguagem Java! Bags podem ser implementados com mapas, mas talvez uma melhor referência seja mais uma vez no “Apache Commons Collections”, onde existe a interface Bag<T> de fato.
Leia com cuidado a documentação dessa interface, porque embora ela herde de Collection<T>, ela não segue a definição de Collection ao pé da letra para todos os métodos, principalmente no “add” e “remove”. A documentação cita quando a especificação de Collection é violada.
E os “Maps”?
Maps, ou mapas, são estruturas de dados que guardam “pares”, ou “entradas” no mapa que chamamos de “chave-valor”. Como as “entradas” não são exatamente os “valores” da coleção, os maps não estão na tabela acima.
Mapas a princípio não possuem noção de ordem sobre as entradas, ou seja, não é verdade que as entradas estão, ou devam estar, em ordem, mesmo que as chaves tenham uma ordem natural, como a ordem alfabética para strings. Vejam o exemplo do mapa “printado” abaixo:
HashMap<String, Integer> map = new HashMap<>();
map.put("one", 1);
map.put("two", 2);
map.put("three", 3);
map.put("four", 4);
System.out.println(map);
Saída:
{four=4, one=1, two=2, three=3}
Observe que a entrada (two=2) foi impressa antes de (three=3), mesmo que “two” venha depois de “three” na ordem alfabética.
A grande característica que torna o mapa tão útil é o acesso do valor pela chave.
Aliás, se não ficou claro, as chaves de um mapa são únicas, não podem se repetir (As chaves de um Map são um Set! Em Java, por exemplo, a interface Map possui um método “keySet” que volta um Set<K>, onde K é o tipo das chaves).
De maneira geral as implementações de mapa providas pelas linguagens são muito rápidas para acessar um valor pela chave. São tempo quase constante (O(1)) para mapas pequenos e provavelmente O(log(n)) para mapas grandes. Além disso, os mapas não permitem duas entradas com a mesma chave, o que torna o acesso de um valor pela chave sem ambiguidade. Mapas se chamam mapas porque eles “mapeiam” chaves em valores. Nesse sentido têm o mesmo objetivo dos métodos “map” do padrão map-reduce de programação funcional.
Importante: nunca esqueça de implementar o método “hashCode” para mapas cuja chave é um VO – Value Object -- customizado. Isso permite que haja o balanceamento das entradas do hash dentro do mapa (HashMap’s). Se você não customizar o hashCode para um mapa cuja chave é um VO, você corre o risco de ter um mapa com performance O(n), ou seja, linear, e muito mais lento do que poderia ser.
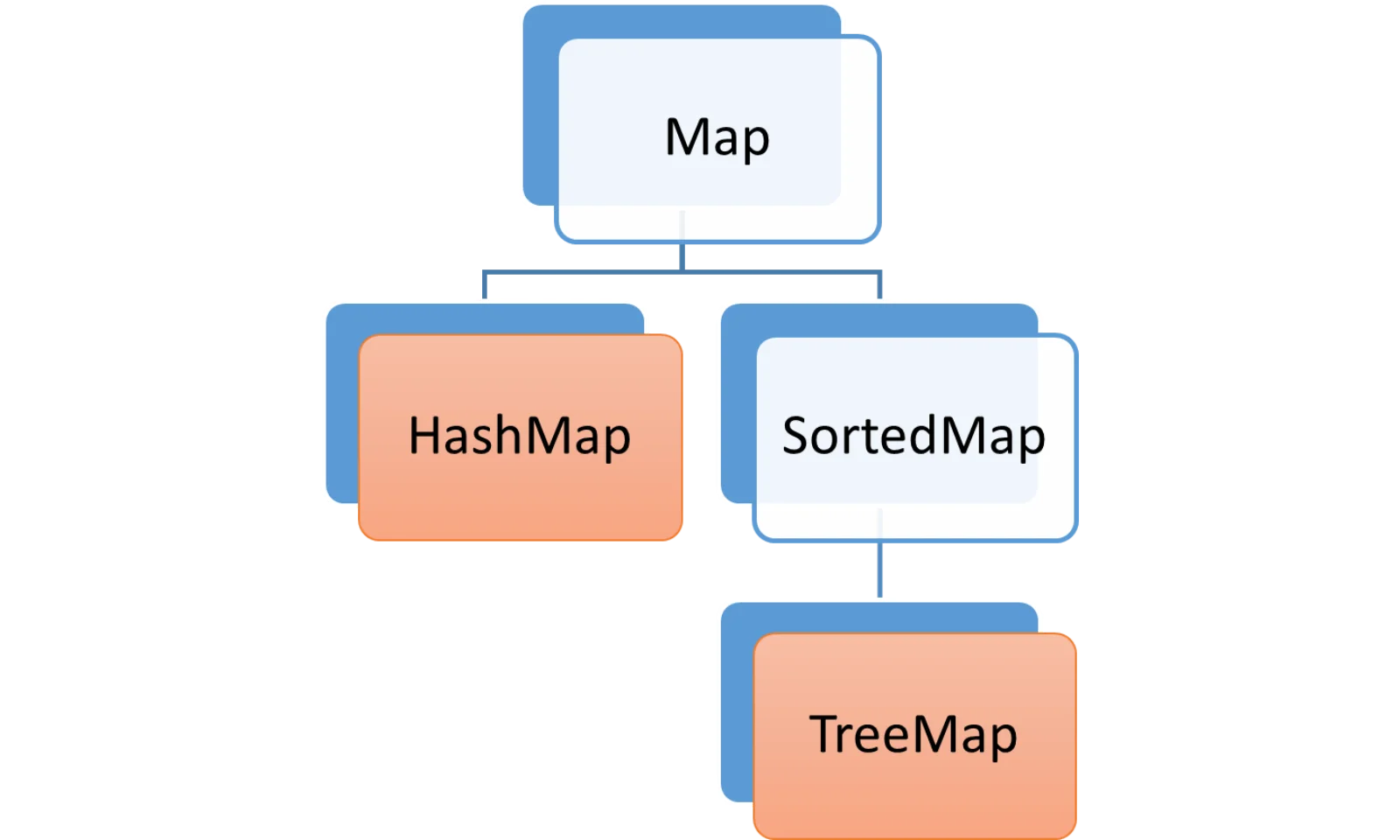
Um mapa, como afirmado, não possui noção de ordem pelas entradas ou chaves. Mas se essa noção for muito importante, você pode procurar se a linguagem entrega um “SortedMap”. Em particular, Java tem essa interface.
Algumas perguntas que podem vir dessa classificação
- Um Bag<T> pode ser implementado como um Map<T,Integer> ?
99%. Talvez seja por isso que não exista o Bag na linguagem Java de partida. Um mapa que leva um determinado objeto, digamos, strings, em inteiros, pode perfeitamente modelar um conjunto de elementos, as chaves do mapa, com as repetições, onde os valores do mapa indicam a quantidade de cada elemento.
O único cuidado, e por isso não é 100%, é que ao usar o método “size” de um mapa, no exemplo, você obterá o número de entradas no mapa e não a soma de elementos com as repetições. No exemplo da urna opaca, se usar um Map, o size voltará 2, mas você pode estar interessado no fato do bag ter 7 elementos e não 2 tipos de elemento. Talvez tenha que iterar o mapa e ir somando os valores, ou carregar essa soma em paralelo da coleção caso obter a soma seja muito crítico e você queira o tempo constante ao invés de linear.
- Um List<T> não poderia ser implementado como um Map<Integer, T>?
Não, porque com o mapa você abre mão da noção de ordem. Veja, um Map<Integer,T> pode ser a estrutura de dados correta para resolver seu problema. A única coisa é que esse mapa usa os inteiros como chaves “normais”, mas não presume a ordem entre elas. Se você está preocupado com uma estrutura de dados que seja esparsa para não ocupar muita memória, mas ainda precisa da noção de ordem, considere usar um LinkedList<T> ao invés do mapa.
- Por que eu usaria um LinkedList<T> ao invés do ArrayList<T>?
Do ponto de vista do acesso posicional, de fato, o ArrayList é (muito) mais rápido que o LinkedList. Arrays acessarão um elemento pela posição em tempo constante enquanto as listas ligadas acessarão em tempo linear.
O possível problema aqui é a memória Se você estiver trabalhando com uma lista muito grande e esparsa (“esparsa” = “poucos elementos de fato preenchidos”), o custo de memória do array será muito maior do que varrer uma lista ligada que só tem os elementos “úteis”.
- Posso raciocinar um Map<K, V> como sendo um Set de pares <K,V> ?
Não exatamente. É verdade que as entradas de um mapa são únicas, o que também é num conjunto de pares (onde a igualdade se mede comparando os dois membros do par), mas a restrição de formação de uma entrada do mapa é mais restrita; ela se dá apenas na chave e não no par chave-valor.
Assim, um conjunto de pares pode ter os pares (x, y) e (x, z), mas um mapa não pode ter essas duas entradas. Ao inserir o par (x, z) num mapa que já tem (x, y), na prática o valor y será substituído por z.
Otimizando um algoritmo usando estruturas de dados
Vamos ver um problema “clássico” de entrevistas para desenvolvedores:
Dado um array de inteiros nums e um inteiro target, retornar um array de dois números contendo índices no array nums tais que a soma deles vale soma.
Você pode voltar qualquer solução válida, caso haja mais de uma, mas você não pode usar o mesmo elemento (índice do array nums) mais de uma vez.
Você pode retornar a resposta em qualquer ordem. Exemplo, se voltar [2,7] ou [7,2] são soluções equivalentes.
Exemplo A: nums = [1,8,0,7,9,3,2,4], target = 6 à Solução: [6,7] ou [7,6]
Exemplo B: nums = [8,9,3,8,3,7], target = 6 à Solução: [2,4] ou [4,2] //[2,2] não serve
Uma solução correta seria fazer dois loops encaixados, digamos, com índices i e j.
Se nums[i] + nums[j] == target, então [i, j] é uma solução.
O problema da solução acima é que ela é quadrática (O(n*n)) em relação ao comprimento do array nums. Se o array for grande, isso pode ser um problema de performance significativo, porque no pior caso teremos essa ordem de grandeza. O exemplo A acima é praticamente o pior caso, onde os elementos que compõem a soma estão no final do array.
Será que conseguimos uma solução linear (O(n)) ou no máximo O(n*log(n))?
A resposta é sim, usando um mapa auxiliar (vamos batizar de “map”). As chaves do mapa serão os valores do array e os valores do mapa serão o índice onde esse valor aparece. O mapa começa vazio.
Então iteramos o array (com índice i) e para cada elemento num[i] verificamos se o mapa contém a chave target-num[i]. Se tiver, então [i, map.get(num[i])] será uma solução. Se não tem, então colocamos (num[i], i) no mapa.
Nessa solução, no pior caso, encontraremos a solução varrendo o array apenas uma vez e não com loop encaixado. Estamos presumindo que a busca de uma chave no mapa é barata, e de fato é.
Fica como exercício vocês implementarem os dois algoritmos acima na linguagem de preferência. Fica também como exercício usarem arrays grandes no teste e avaliarem a diferença de performance no pior caso.
Conclusão
Neste post foram apresentadas algumas estruturas de dados e alguns critérios de caracterização para escolher a “melhor” estrutura que resolva determinado problema.
Uma nota importante: não deixe de implementar o método “equals” para coleções de objetos compostos (VO’s – Value Object’s). Se você não fizer isso, as regras de pertencimento de um elemento na coleção e de não-repetição no caso dos Sets não serão aplicadas corretamente. Para String, Integer, Long, etc., isso não é necessário porque essas classes já implementam o método equals.
Observe que um problema pode ter soluções equivalentes em termos de performance usando combinações diferentes de estruturas de dados. A lição que fica aqui é procurar a melhor usando dados e não “achismos”, e a performance do algoritmo é o dado mais importante. No mundo real apenas o algoritmo correto não basta. Faça POCs com implementações diferentes do mesmo algoritmo e compare os resultados. Otimizar um algoritmo é bem melhor do que provisionar mais máquina para ter mais capacidade computacional.
Não deixe de escrever os testes unitários dos seus algoritmos. Inclusive testes unitários avançados podem avaliar performance, como por exemplo, “quero que com esses dados o cálculo demore menos de 30ms” e se passar desse tempo o teste não passa. Alguns sites de avaliação de questões para desenvolvedores de fato fazem isso.
Num mundo com mais serverless, como as “functions” dos provedores de cloud, otimizar algoritmos fica ainda mais importante, porque ela refletirá diretamente no custo, não só com a visão técnica da ordem de complexidade, mas também financeira. Função que roda mais lenta, custa mais caro, simples assim.
Referências
Links javadoc
https://docs.oracle.com/javase/8/docs/api/java/util/Collection.html
https://docs.oracle.com/javase/8/docs/api/java/util/List.html
https://docs.oracle.com/javase/8/docs/api/java/util/Set.html
https://docs.oracle.com/javase/8/docs/api/java/util/SortedSet.html
https://docs.oracle.com/javase/8/docs/api/java/util/Map.html
https://docs.oracle.com/javase/8/docs/api/java/util/SortedMap.html
Apache Commons Collections
https://commons.apache.org/proper/commons-collections/
LeetCode
https://leetcode.com/problems/two-sum/






